2022 Impact Factor: 3.0
SCImago Journal & Country Rank

Related Articles

Direct Detection of Escherichia coli, Staphylococcus aureus, and Salmonella spp. in Animal-derived Foods Using a Magnetic Bead-based Immunoassay
Korean J Food Sci Anim Resour 2018;38(4):727-736.

Highlighting the Microbial Community of Kuflu Cheese, an Artisanal Turkish Mold-Ripened Variety, by High-Throughput Sequencing
Food Sci Anim Resour 2024;44(2):390-407.

Highlighting the microbial community of Kuflu cheese, an artisanal Turkish mold-ripened variety, by high-throughput sequencing
Food Sci Anim Resour 2023 [published online ahead of print: Sep 21, 2023]

Bactericidal Effect of Combination of Atmospheric Pressure Plasma and Nisin on Meat Products Inoculated with Escherichia coli O157:H7
Food Sci Anim Resour 2023;43(3):402-411.

Inhibition of Listeria monocytogenes in Fresh Cheese Using a Bacteriocin-Producing Lactococcus lactis CAU2013 Strain
Food Sci Anim Resour 2022;42(6):1009-1019.



2017; 37(4):579-592

pISSN: 1225-8563, eISSN: 2234-246X

DOI: https://doi.org/10.5851/kosfa.2017.37.4.579

ARTICLE

Microbial Risk Assessment of Non-Enterohemorrhagic Escherichia coli in Natural and Processed Cheeses in Korea

Kyungmi Kim1,†, Heeyoung Lee†, Soomin Lee, Sejeong Kim, Jeeyeon Lee, Jimyeong Ha, Yohan Yoon*
Author Information & Copyright ▼
Risk Analysis Research Center, Sookmyung Women’s University, Seoul 04310
1Department of Food and Nutrition, Sookmyung Women’s University, Seoul 04310, Korea
†Kyungmi Kim and Heeyoung Lee are equally contributed.
*Corresponding author Yohan Yoon Department of Food and Nutrition, Sookmyung Women’s University, Seoul 04310, Korea Tel: +82-2-2077-7585 Fax: +82-2-710-9479 E-mail: yyoon@sookmyung.ac.kr

Copyright © 2017, Korean Society for Food Science of Animal Resources. This is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jun 09, 2017 ; Revised: Aug 06, 2017 ; Accepted: Aug 07, 2017

Published Online: Aug 31, 2017

Abstract

This study assessed the quantitative microbial risk of non-enterohemorrhagic Escherichia coli (EHEC). For hazard identification, hazards of non-EHEC E. coli in natural and processed cheeses were identified by research papers. Regarding exposure assessment, non-EHEC E. coli cell counts in cheese were enumerated, and the developed predictive models were used to describe the fates of non-EHEC E. coli strains in cheese during distribution and storage. In addition, data on the amounts and frequency of cheese consumption were collected from the research report of the Ministry of Food and Drug Safety. For hazard characterization, a dose-response model for non-EHEC E. coli was used. Using the collected data, simulation models were constructed, using software @RISK to calculate the risk of illness per person per day. Non-EHEC E. coli cells in natural- (n=90) and processed-cheese samples (n=308) from factories and markets were not detected. Thus, we estimated the initial levels of contamination by Uniform distribution × Beta distribution, and the levels were −2.35 and −2.73 Log CFU/g for natural and processed cheese, respectively. The proposed predictive models described properly the fates of non-EHEC E. coli during distribution and storage of cheese. For hazard characterization, we used the Beta-Poisson model (α=2.21×10−1, N50=6.85×107). The results of risk characterization for non-EHEC E. coli in natural and processed cheese were 1.36×10−7 and 2.12×10−10 (the mean probability of illness per person per day), respectively. These results indicate that the risk of non-EHEC E. coli foodborne illness can be considered low in present conditions.

Keywords: microbial risk assessment; Escherichia coli; cheese; exposure assessment

Introduction

Cheese consumption has been increasing gradually in Korea since the 1990s (KDC, 2016), but the cases of contamination with Listeria monocytogenes, Staphylococcus aureus, and Escherichia coli have been reported (Jo et al., 2007; Tekinsen and Özdemir, 2006; Thayer et al., 1998). Especially, E. coli has been isolated from various cheeses in many countries (Haran et al., 2011; Zinke et al., 2012).

E. coli, a facultative anaerobic Gram-negative bacillus, is commonly found in the intestinal flora of humans and animals, and certain strains are pathogenic (MFDS, 2010; Olsvik et al., 1991). According to infection symptoms and pathogenesis, pathogenic E. coli strains are classified e.g., enteropathogenic E. coli (EPEC), enteroinvasive E. coli (EIEC), enterotoxigenic E. coli (ETEC), enterohemorrhagic E. coli (EHEC), and enteroaggregative E. coli (EAEC) (Nataro and Kaper, 1998; Yoon, 2009). Among the pathogenic E. coli strains, E. coli O157:H7 is one of the major concerns in the dairy industry, and the survival of the pathogens in various cheeses has been well documented (Griffin and Tauxe, 1991; Reitsma and Henning, 1996). Thus, several countries (EU, USA, and Canada) have a quantitative standard or “zero tolerance” policy for control of the pathogens in cheese (EC, 2005; FDA, 2009; Health Canada, 2008); several microbiological risk assessments for E. coli O157:H7 in cheese have also been conducted (FSANZ, 2009; Perrin et al., 2015). However, microbial risk assessment for non-EHEC E. coli in cheese has not been conducted. Hence, there is a lack of scientific evidence to determine microbial risk of non-EHEC E. coli.

EPA (2012) recommends microbiological risk assessment to evaluate the risk posed by bacteria, to prevent foodborne illnesses, and to identify environmental factors influencing microbial growth. The microbiological risk assessment should include hazard identification, exposure assessment, hazard characterization, and risk characterization (Codex, 1999).

The objective of this study was to conduct microbial risk assessment for non-EHEC E. coli in natural cheese which is manufactured from milk fermentation by adding start culture enzyme, and salt and processed cheeses which are manufactured from natural cheese using emulsifiers in Korea.

Materials and Methods

Hazard identification

To identify the hazards of E. coli, the general characteristics and foodborne-illness outbreaks linked to E. coli in cheese were collected from other studies.

Exposure assessment
Prevalence of E. coli

To evaluate non-EHEC E. coli prevalence and the contamination level, natural- (n=90) and processed-cheese samples (n=308) were collected from various cheese factories and markets. At two factories, samples were collected throughout the manufacturing process from raw milk to packaged cheese. Natural-cheese samples were collected from raw milk, pasteurized milk, cheese before ripening, cheese after packaging, cheese before shipping, and markets. Processed-cheese samples were also collected after packaging, before shipping, and in markets. In addition, distributed cheeses were collected from local markets in five cities in Korea. Cheese samples were evaluated in both summer and winter to reduce the effect of external environmental factors such as temperature, humidity and contamination levels of the pathogen. The collected samples were placed in an ice cooler and were transported to a laboratory. One-milliliter samples of raw milk and pasteurized milk were serially diluted with 0.1% buffered peptone water (BPW; Becton, Dickinson, and Company, USA). The diluents were then surface-plated on tryptic soy agar (TSA; Becto, Dickinson, and Company) and E. coli /Coliform Count petrifilm (3M™, USA) to quantify total bacteria, and non-EHEC E. coli and coliform counts, respectively. In addition, 25 g or 1 slice of cheese was aseptically transferred into a sample bag (3M™), and 25 mL of BPW was added, and the mixture was homogenized for 120 s with a pummeler (Bag-Mixer®, Interscience, France). One milliliter of the homogenate was serially diluted with BPW, and 0.1-mL diluents for TSA and 1-mL diluents for non-EHEC E. coli / Coliform Count petrifilm (3M™) were then surface-plated, respectively. The plates and petrifilms were incubated at 35°C for 24 h, and then the colonies were manually counted.

Initial level of contamination with non-EHEC E. coli

Beta distribution is a continuous probability distribution parametrized by two shape parameters (α1 and α2), and the interval of the distribution is zero to one (Johnson et al., 1995). When the number of positive samples is low, beta distribution can be used to estimate bacterial prevalence. The data on non-EHEC E. coli prevalence in cheese were fitted to a Beta distribution (α1, α2), where α1 is the number of positive samples + 1, and α2 is the number of all tested samples - positive samples + 1 (Vose, 1998). Uniform distribution is also a continuous probability distribution defined by the two parameters (a and b), and the distribution indicates equal probability in the range of two parameters. Because non-EHEC E. coli were detected under detection limit, initial concentration was assumed in the range of zero to detection limit. Thus, the data on the non-EHEC E. coli contamination level in cheese from cheese factory storage were fitted to a Uniform distribution (a, b), where a is the minimal contamination level, and b is the maximal contamination level. Finally, the initial contamination level (Log CFU/g) was calculated by prevalence × contamination level using the @RISK software, version 5.7 (Palisade Corp., USA).

Non-EHEC E. coli growth during distribution and storage

To calculate non-EHEC E. coli growth during distribution and storage, predictive models for natural and processed cheeses from a study by MFDS (2013) were used as follows.

<Natural cheese>

μ max = [ 0.00268 × ( T – 5.4235 ) ] 2
(1)

L P D = [ 1 ( – 0.0522 + 0.0142 × T ) ] 2
(2)

<Processed cheese>

μ max =0.036 − 0.0030 × T + 0.0004 × T 2
(3)

L P D = [ 1 ( – 0.0826 + 0.0275 × T ) ] 2
(4)

The μmax (Log CFU/g) is the maximum specific growth rate, LPD (h) is lag phase duration, and T (°C) is temperature. In addition, to simulate non-EHEC E. coli growth under changing temperature and time, probabilistic distributions for temperature and time from a study by Lee et al. (2015) were used.

Cheese consumption

Data on cheese consumption and intake frequency of cheese were taken from the study of Lee et al. (2015) to calculate the non-EHEC E. coli risk as a result of cheese consumption in Korea. According to a study by Lee et al. (2015), the mean consumption amounts of natural cheese and processed cheese are 12.40±19.43 g/d (95% confidence interval: 0.915−34.90 g/d) and 19.46±14.39 g/d (95% confidence interval: 2.6−40.0 g/d), respectively, and the consumption frequencies of cheese are 0.0389 and 0.0232 for natural and processed cheese, respectively. The ratios were fitted to the Discrete distribution{(0,1), [1 − (daily frequency of consumption), daily frequency of consumption]} (Lee et al., 2015). Finally, ingested E. coli cell counts were calculated as a result of consuming natural or processed cheese from the final concentration at the time of consumption taking into account the consumption amount and frequency.

The dose-response model

Twenty-eight dose-response models for E. coli infection were surveyed from other studies. Because about 90% of E. coli foodborne illness in Korea occurred by EPEC (Hong et al., 2005), the following dose-response model developed by Powell et al. (2000) for EPEC was used in this study.

P = 1 − { 1 + ( D × [ ( 2 1 / α − 1 ) ] N 50 ) } − α
(5)

Where P is the probability of illness, D is the ingested E. coli cell number (CFU/serving), N50 is the dose infecting 50% of the population with E. coli, and α is a coefficient.

Risk characterization

The results of the exposure assessment, dose-response model, and cheese consumption amount and frequency were used to estimate the risk of non-EHEC E. coli in cheese by means of a simulation in software @RISK according to the scheme of the simulation model in Fig. 1. In the simulation for risk characterization, the sampling type was Median Latin Hypercube, and the generator seed was random with settings for 10,000 iterations. Tables 1 and 2 show simulation models and formulas for calculating the risk of non-EHEC E. coli in natural and processed cheeses by means of @RISK. Sensitivity analysis to determine factors influencing the risk was also conducted in @RISK.

kosfa-37-4-579-f001
Fig. 1. Fitted Beta distribution (A) and probability density (B) of the simulated initial level of contamination with Escherichia coli in natural cheese.
Download Original Figure

Table 1. The simulation model and formulas in a Microsoft Excel® spreadsheet used to calculate the risk of illness of Escherichia coli in natural cheese by means of the @RISK software
Input Model Unit Code Formula References
PRODUCT
Product
Pathogen Contamination
level
Non-EHEC E. coli PR =RiskBeta(1,91) Vose (1998)
prevalence
Concentration CFU/g C =RiskUniform(0,2) Vose (1998)
Initial contamination level CFU/g IC =PR×C Vose (1998)
Log CFU/g log(IC) =log(PR×C)
TRANSPORTATION
Transportation time h timetrans =RiskPert(1,3,6) Personal communicationa
Food temperature °C temptrans =RiskPert(0,4,10) Personal communicationa
during transportation
Download Excel Table

Table 1. The simulation model and formulas in a Microsoft Excel® spreadsheet used to calculate the risk of illness of Escherichia coli in natural cheese by means of the @RISK software
Input Model Unit Code Formula References
Growth
h0 Log CFU/g h0 =average(growth rate×lag time), Fixed 2.26 MFDS (2013),
Baranyi and Roberts (1994)
Y0 Log CFU/g Y0 =average(Y0i), Fixed 3.36 MFDS (2013),
Baranyi and Roberts (1994)
Yend Log CFU/g Yend =average(Yendi), Fixed 9.04 MFDS (2013),
Baranyi and Roberts (1994)
ln(q) ln(q) =LN{1/[EXP(h0)−1]} MFDS (2013),
Baranyi and Roberts (1994)
Lag time h TransLt =IF{Temptrans>4, MFDS (2013)
  [1/(−0.0522+0.0142×Temptrans)]2, 1320}
Growth rate Log CFU/g/h TransGr =IF{Temptrans>5.4235, MFDS (2013)
  [0.0268×(Temptrans−5.4235)]2, 0} Ratkowsky et al. (1982)
Non-EHEC Log CFU/g C1 =IC+1/{1+EXP[−ln(q)]}× MFDS (2013)
E. coli growth   [1−10−|Y0−Yend|/LN(10)]×TransGr×timetrans Baranyi and Roberts (1994)
MARKET
Market storage
Storage time h Mark-timest =RiskPert(0,2,48) Personal communicationb
Food temperature °C Mark-Tempst =RiskUniform(2,4) Personal communicationb
during storage
Growth
h0 Log CFU/g h0 =average(growth rate×lag time), Fixed 2.26 MFDS (2013),
Baranyi and Roberts (1994)
Y0 Log CFU/g Y0 =average(Y0i), Fixed 3.36 MFDS (2013),
Baranyi and Roberts (1994)
Yend Log CFU/g Yend =average(Yendi), Fixed 9.04 MFDS (2013),
Baranyi and Roberts (1994)
ln(q) ln(q) =LN{1/[EXP(h0)−1]} MFDS (2013),
Baranyi and Roberts (1994)
Lag time h Markst−TimeLt =IF{Mark−Tempst>4, MFDS (2013)
  [1/(−0.0522+0.0142×Mark−Tempst)]2, 1320}
Growth rate Log CFU/g/h Markst−RGr =IF{Mark−Tempst>5.4235, MFDS (2013)
  [0.0268×(Mark−Tempst−5.4235)]2, 0} Ratkowsky et al. (1982)
Non-EHEC Log CFU/g C2−1 =C1+1/{1+EXP[−ln(q)]}×[1−10−|Y0−end|/ MFDS (2013)
E. coli growth   LN(10)]×Markst−RGr×Mark−timest Baranyi and Roberts (1994)
Market display
Storage time h Mark-timedis =RiskPert(0,48,168) Personal communicationb
Food temperature °C Mark-Tempdis =RiskTriang(0.60703,4.1000,15.18) Lee et al. (2015)
during storage
Growth
h0 Log CFU/g h0 =average(growth rate×lag time), Fixed 2.26 MFDS (2013),
Baranyi and Roberts (1994)
Y0 Log CFU/g Y0 =average(Y0i), Fixed 3.36 MFDS (2013),
Baranyi and Roberts (1994)
Yend Log CFU/g Yend =average(Yendi), Fixed 9.04 MFDS (2013),
Baranyi and Roberts (1994)
ln(q) ln(q) =LN{1/[EXP(h0)−1]} MFDS (2013),
Baranyi and Roberts (1994)
Lag time h Markdis−TimeLt =IF{Mark−Tempdis>4, MFDS (2013)
  [1/(−0.0522+0.0142×Mark−Tempdis)]2, 1320}
Growth rate Log CFU/g/h Markdis−RGr =IF{Mark−Tempdis>5.4235, MFDS (2013)
  [0.0268×(Mark−Tempdis−5.4235)]2, 0} Ratkowsky et al. (1982)
Non-EHEC Log CFU/g C2 =(C2−1)+1/{1+EXP[−ln(q)]}×[1−10−|Y0−end|/ MFDS (2013)
E. coli growth   LN(10)]×Markdis−RGr×Mark−timedis Baranyi and Roberts (1994)
Download Excel Table

Table 1. The simulation model and formulas in a Microsoft Excel® spreadsheet used to calculate the risk of illness of Escherichia coli in natural cheese by means of the @RISK software
Input Model Unit Code Formula References
TRANSPORTATION (CAR)
Transportation
(CAR) storage
Transportation time h timecar =RiskPert(0.325,0.984,1.643) Jung (2011)
Food temperature °C Tempcar =RiskPert(10,18,25) Jung (2011)
during transportation
Growth
h0 Log CFU/g h0 =average(growth rate×lag time), Fixed 2.26 MFDS (2013),
Baranyi and Roberts (1994)
Y0 Log CFU/g Y0 =average(Y0i), Fixed 3.36 MFDS (2013),
Baranyi and Roberts (1994)
Yend Log CFU/g Yend =average(Yendi), Fixed 9.04 MFDS (2013),
Baranyi and Roberts (1994)
ln(q) ln(q) =LN{1/[EXP(h0)−1]} MFDS (2013),
Baranyi and Roberts (1994)
Lag time h Car-TimeLt =IF{Tempcar>4, MFDS (2013)
  [1/(−0.0522+0.0142×Tempcar)]2, 1320}
Growth rate Log CFU/g/h Car−RGr =IF{Tempcar>5.4235, MFDS (2013)
  [0.0268×(Tempcar−5.4235)]2, 0} Ratkowsky et al. (1982)
Non-EHEC Log CFU/g C3 =C2+1/{1+EXP[−ln(q)]}×[1−10−|Y0−Yend|/ MFDS (2013)
E. coli growth   LN(10)]×Car−RGr×timecar Baranyi and Roberts (1994)
HOME
Home storage
Storage time h Home-timest RiskNormal[250.1742, 176.0175, Lee et al. (2015)
  RiskTruncate(0,4320)]
Food temperature °C Home-Tempst =RiskLogLogistic[-29.283, 33.227, 26.666, Lee et al. (2015)
during storage   RiskTruncate(−5,20)]
Growth
h0 Log CFU/g h0 =average(growth rate×lag time), Fixed 2.26 MFDS (2013),
Baranyi and Roberts (1994)
Y0 Log CFU/g Y0 =average(Y0i), Fixed 3.36 MFDS (2013),
Baranyi and Roberts (1994)
Yend Log CFU/g Yend =average(Yendi), Fixed 9.04 MFDS (2013),
Baranyi and Roberts (1994)
ln(q) ln(q) =LN{1/[EXP(h0)−1]} MFDS (2013),
Baranyi and Roberts (1994)
Lag time h Home−TimeLt =IF{Home−Tempst>4, MFDS (2013)
  [1/(−0.0522+0.0142×Home−Tempst)]2, 1320}
Growth rate Log CFU/g/h Home−RGr =IF{Home−Tempst>5.4235, MFDS (2013)
  [0.0268×(Home−Tempst−5.4235)]2, 0} Ratkowsky et al. (1982)
Non-EHEC Log CFU/g C4 =C3+1/{1+EXP[−ln(q)]}×[1−10−|Y0−Yend|/ MFDS (2013)
E. coli growth   LN(10)]×Home−RGr×Home−timest Baranyi and Roberts (1994)
CONSUMPTION
Daily consumption g Consump =RiskPearson5[2.6488, 25.81, MFDS (2013)
average amount   RiskTruncate(0,100),RiskShift(-3.2572)]
Daily consumption % ConFre Fixed 3.894 MFDS (2013)
frequency
CF(0) =1−3.894/100 MFDS (2013),
CF(1) =3.894/100 MFDS (2013),
CF =RiskDiscrete[{0,1},{CF(0),CF(1)}] MFDS (2013),
ConFre =IF(CF=0,0,Consump) MFDS (2013),
DOSE-RESPONSE
Non-EHEC E. coli amount D =10C4×ConFre
Parameter of α α =Fixed 2.21×10−1 Powell (2000)
Parameter of N50 N50 =Fixed 6.85×107 Powell (2000)
RISK
Probability of Risk =1−(1+{D×[(21/α)−1]/N50})−α Powell (2000)
illness/person/day

aWith a supervisor of a cheese manufacturing plant

bWith a manager in charge of cheese products at markets

Download Excel Table

Table 2. The simulation model and formulas in a Microsoft Excel® spreadsheet used to calculate the risk of Escherichia coli in processed cheese by means of the @RISK software
Input Model Unit Code Formula References
PRODUCT
Product
Pathogen Contamination
level
Non-EHEC E. coli PR =RiskBeta(1,309) Vose (1998)
prevalence
Concentration CFU/g C =RiskUniform(0,2.8) Vose (1998)
Initial contamination level CFU/g IC =PR×C Vose (1998)
Log CFU/g log(IC) =log(PR×C)
TRANSPORTATION
Transportation time h timetrans =RiskPert(1,3,6) Personal communicationa
Food temperature °C Temptrans =RiskPert(0,4,10) Personal communicationa
during transportation
Growth
h0 Log CFU/g h0 =average(growth rate×lag time), Fixed 0.65 MFDS (2013),
Baranyi and Roberts (1994)
Y0 Log CFU/g Y0 =average(Y0i), Fixed 3.11 MFDS (2013),
Baranyi and Roberts (1994)
Yend Log CFU/g Yend =average(Yendi), Fixed 7.32 MFDS (2013),
Baranyi and Roberts (1994)
ln(q) ln(q) =LN{1/[EXP(h0)−1]} MFDS (2013),
Baranyi and Roberts (1994)
Lag time h TransLt =IF{Temptrans>4, MFDS (2013)
  [1/(−0.0826+0.0275×Tempcar)]2, 1320}
Growth rate Log CFU/g/h TransGr =IF(Temptrans>8.6,0.0036−0.0030×Temptrans+ MFDS (2013)
  0.0004×Temptrans2, 0) Ratkowsky et al. (1982)
Non-EHEC Log CFU/g C1 =IC+1/{1+EXP[−ln(q)]}×[1−10−|Y0−Yend|/ MFDS (2013)
E. coli growth   LN(10)]×TransGr×timetrans Baranyi and Roberts (1994)
MARKET
Market storage
Storage time h Market-timest =RiskPert(0,2,48) Personal communicationb
Food temperature °C Mark-Tempst =RiskUniform(2,4) Personal communicationb
during storage
Growth
h0 Log CFU/g h0 =average(growth rate×lag time), Fixed 0.65 MFDS (2013),
Baranyi and Roberts (1994)
Y0 Log CFU/g Y0 =average(Y0i), Fixed 3.11 MFDS (2013),
Baranyi and Roberts (1994)
Yend Log CFU/g Yend =average(Yendi), Fixed 7.32 MFDS (2013),
Baranyi and Roberts (1994)
ln(q) ln(q) =LN{1/[EXP(h0)−1]} MFDS (2013),
Baranyi and Roberts (1994)
Lag time h Markst−TimeLt =IF{Mark−Tempst>4, MFDS (2013)
  [1/(−0.0826+0.0275×Mark−Tempst)]2, 1320}
Growth rate Log CFU/g/h Markst−RGr =IF(Mark−Tempst>8.6,0.0036−0.0030× MFDS (2013)
  Mark−Tempst+0.0004×Mark−Tempst2, 0) Ratkowsky et al. (1982)
Non-EHEC Log CFU/g C2−1 =C1+1/{1+EXP[−ln(q)]}×[1−10−|Y0−Yend|/ MFDS (2013)
E. coli growth   LN(10)]×Mark−RGr×Mark−timest Baranyi and Roberts (1994)
Market display
Storage time h Mark−timedis =RiskPert(0,48,168) Personal communicationb
Food temperature °C Mark−Tempdis =RiskTriang(0.60703,4.1000,15.18) Lee et al. (2015)
during storage
Growth
h0 Log CFU/g h0 =average(growth rate×lag time), Fixed 0.65 MFDS (2013),
Baranyi and Roberts (1994)
Download Excel Table

Table 2. The simulation model and formulas in a Microsoft Excel® spreadsheet used to calculate the risk of Escherichia coli in processed cheese by means of the @RISK software
Input Model Unit Code Formula References
Y0 Log CFU/g Y0 =average(Y0i), Fixed 3.11 MFDS (2013),
Baranyi and Roberts (1994)
Yend Log CFU/g Yend =average(Yendi), Fixed 7.32 MFDS (2013),
Baranyi and Roberts (1994)
ln(q) ln(q) =LN{1/[EXP(h0)−1]} MFDS (2013),
Baranyi and Roberts (1994)
Lag time h Markdis−TimeLt =IF{Mark−Tempdis>4, MFDS (2013)
  [1/(−0.0826+0.0275×Mark−Tempdis)]2, 1320}
Growth rate Log CFU/g/h Markdis−RGr =IF(Mark−Tempdis>8.6,0.0036−0.0030× MFDS (2013)
  Mark−Tempdis+0.0004×Mark−Tempdis2, 0) Ratkowsky et al. (1982)
Non-EHEC Log CFU/g C2 =(C2−1)+1/{1+EXP[−ln(q)]}×[1−10−|Y0−Yend|/ MFDS (2013)
E. coli growth   LN(10)]×Markdis−RGr×Mark−timedis Baranyi and Roberts (1994)
TRANSPORTATION (CAR)
Transportation
(CAR) storage
Transportation time h timecar =RiskPert(0.325,0.984,1.643) Jung (2011)
Food temperature °C Tempcar =RiskPert(10,18,25) Jung (2011)
during transportation
Growth
h0 Log CFU/g h0 =average(growth rate×lag time), Fixed 0.65 MFDS (2013),
Baranyi and Roberts (1994)
Y0 Log CFU/g Y0 =average(Y0i), Fixed 3.11 MFDS (2013),
Baranyi and Roberts (1994)
Yend Log CFU/g Yend =average(Yendi), Fixed 7.32 MFDS (2013),
Baranyi and Roberts (1994)
ln(q) ln(q) =LN{1/[EXP(h0)−1]} MFDS (2013),
Baranyi and Roberts (1994)
Lag time h Car−TimeLt =IF{Tempcar>4, MFDS (2013)
  [1/(−0.0826+0.0275×Tempcar)]2, 1320}
Growth rate Log CFU/g/h Car−RGr =IF(Tempcar>8.6, MFDS (2013)
  0.0036−0.0030×Tempcar+0.0004×Tempcar2, 0) Ratkowsky et al. (1982)
Non-EHEC Log CFU/g C3 =C2+1/{1+EXP[−ln(q)]}×[1−10−|Y0−Yend|/ MFDS (2013)
E. coli growth   LN(10)]×Car−RGr×timecar Baranyi and Roberts (1994)
HOME
Home storage
Storage time h Home−timest =RiskNormal[250.1742, 176.0175, Lee et al. (2015)
RiskTruncate(0,4320)]
Food temperature °C Home−Tempst =RiskLogLogistic[-29.283, 33.227, 26.666, Lee et al. (2015)
during storage RiskTruncate(−5,20)]
Growth
h0 Log CFU/g h0 =average(growth rate×lag time), Fixed 0.65 MFDS (2013),
Baranyi and Roberts (1994)
Y0 Log CFU/g Y0 =average(Y0i), Fixed 3.11 MFDS (2013),
Baranyi and Roberts (1994)
Yend Log CFU/g Yend =average(Yendi), Fixed 7.32 MFDS (2013),
Baranyi and Roberts (1994)
ln(q) ln(q) =LN{1/[EXP(h0)−1]} MFDS (2013),
Baranyi and Roberts (1994)
Lag time h Home−TimeLt =IF{Home−Tempst>4, MFDS (2013)
  [1/(−0.0826+0.0275×Home−Tempst)]2, 1320}
Growth rate Log CFU/g/h Home−RGr =IF(Home−Tempst>8.6,0.0036−0.0030× MFDS (2013)
  Home−Tempst+0.0004×Home−Tempst2,0) Ratkowsky et al. (1982)
Non-EHEC Log CFU/g C4 =C3+1/{1+EXP[−ln(q)]}×[1−10−|Y0−Yend|/ MFDS (2013)
E. coli growth   LN(10)]×Home−RGr×Home−timest Baranyi and Roberts (1994)
Download Excel Table

Table 2. The simulation model and formulas in a Microsoft Excel® spreadsheet used to calculate the risk of Escherichia coli in processed cheese by means of the @RISK software
Input Model Unit Code Formula References
CONSUMPTION
Daily consumption g Consump =RiskWeibull[1.3482, 20.932, MFDS (2013),
average amount  RiskShift(0.26384),RiskTruncate(0,100)]
Daily consumption % ConFre Fixed 2.323 MFDS (2013)
frequency
CF(0) =1−2.323/100 MFDS (2013)
CF(1) =2.323/100 MFDS (2013)
CF =RiskDiscrete{[0,1],[CF(0),CF(1)]} MFDS (2013)
ConFre =IF(CF=0,0,Consump) MFDS (2013)
DOSE-RESPONSE
Non-EHEC E. coli amount D =10C4×ConFre
Parameter of α α =Fixed 2.21×10−1 Powell (2000)
Parameter of N50 N50 =Fixed 6.85×107 Powell (2000)
RISK
Probability of Risk =1−(1+{D×[(21/α)−1]/N50})−α Powell (2000)
illness/person/day

aWith a supervisor of a cheese manufacturing plant

bWith a manager in charge of cheese products at markets

Download Excel Table

Results and Discussion

Hazard identification of E. coli in cheese

Pathogenic E. coli causes diarrhea in infants or acute enteritis in adults (MFDS, 2010). Although ground beef and fresh vegetables are considered major vectors for pathogenic E. coli (MFDS, 2010), there are several reports about E. coli isolated from various cheeses in many countries. The most frequently isolated E. coli serotype in cheese is E. coli O157:H7 in many countries (BCCDC, 2013; CDC, 2010; Honish et al., 2005), but other pathotypes such as EPEC, ETEC, and EAEC were also isolated from various cheeses (Baranceli et al., 2014; Bonyadian et al., 2014; Najand and Ghanbarpour, 2006). In addition, the most frequently isolated pathotype in Korea in various foods is EPEC (Hong et al., 2015). Thus, after non-EHEC E. coli was identified as a hazard in cheese, subsequent quantitative microbial risk assessment for natural and processed cheeses was conducted.

Initial level of non-EHEC E. coli

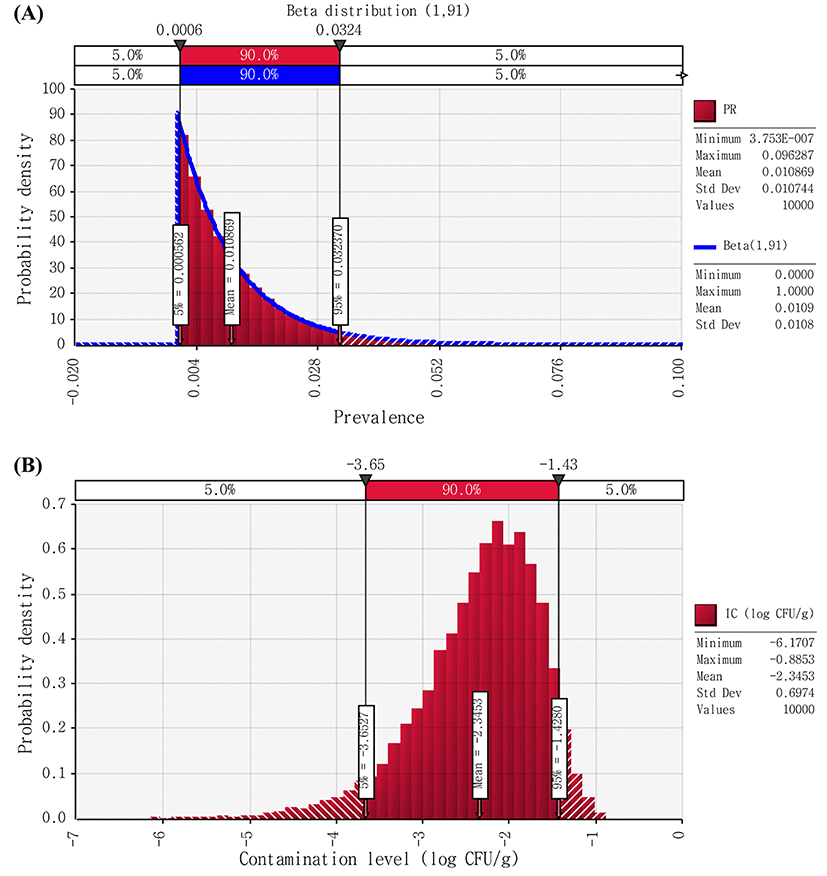
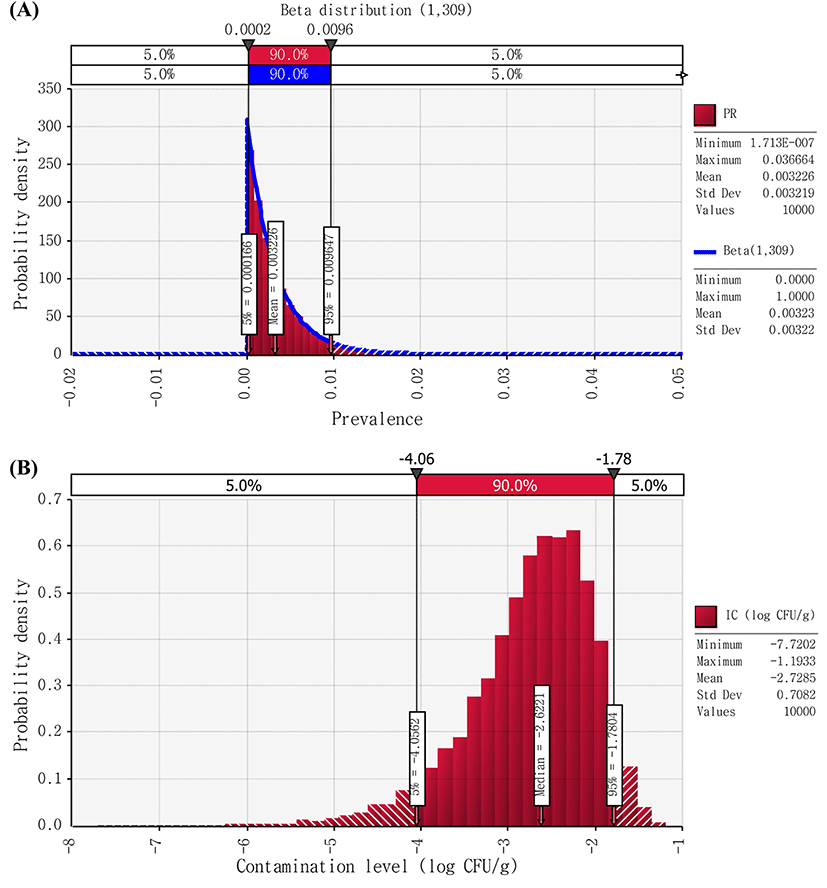
Non-EHEC E. coli cell counts were found to be below the detection limit (natural cheese: 2 CFU/g; processed cheese: 2.8 CFU/g) in all samples. Thus, it was assumed that non-EHEC E. coli cell counts in cheese to be above 0 CFU/g, but below the detection limit (2 CFU/g), and then we described contamination levels of the pathogen with Uniform distribution (0,2) and Uniform distribution (0,2.8) for natural and processed cheese, respectively (Figs. 2 and 3). Therefore, using the @RISK software, the initial contamination level of non-EHEC E. coli were calculated by Beta distribution(1,91) × Uniform distribution(0,2), and Beta distribution(1,309) × Uniform distribution(0,2.8) for natural and processed cheese, respectively. As a result of the simulation, the initial level of contamination with non-EHEC E. coli in cheese was 2.35 and −2.73 Log CFU/g for natural and processed cheese, respectively (Figs. 2 and 3).

kosfa-37-4-579-f002
Fig. 2. Fitted Beta distribution (A) and probability density (B) of the simulated initial level of contamination with Escherichia coli in processed cheese.
Download Original Figure
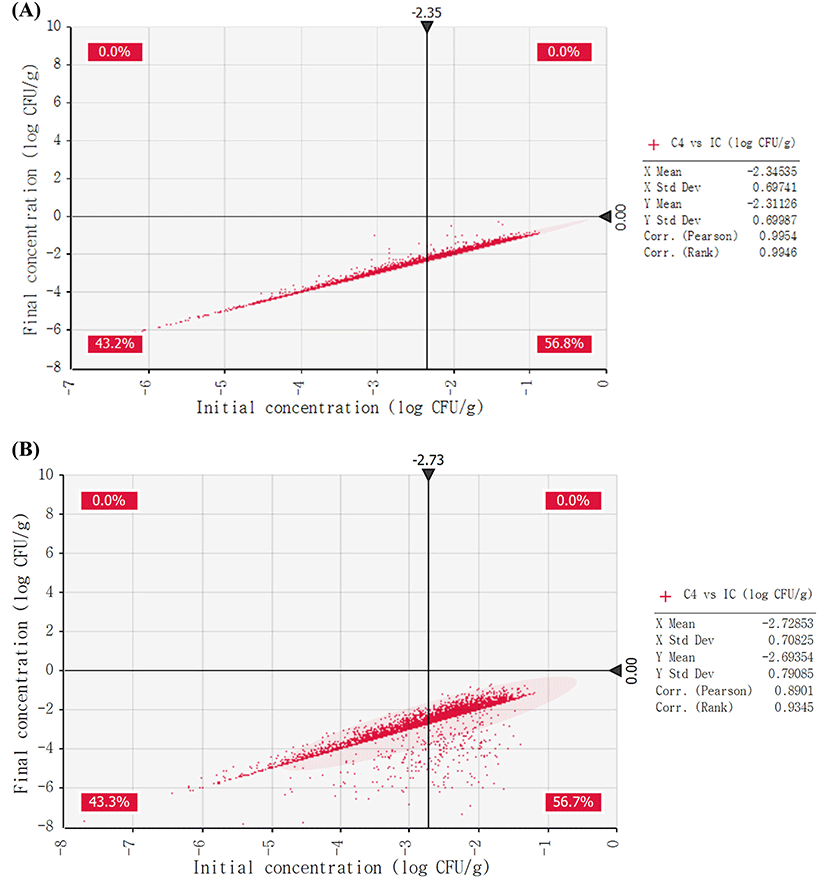
kosfa-37-4-579-f003
Fig. 3. The scatter plots of the initial concentration level versus the home consumption level in terms of Escherichia coli in natural (A) and processed cheese (B).
Download Original Figure
Non-EHEC E. coli growth and cheese consumption

The cumulative distributions of non-EHEC E. coli growth during distribution and storage (initial concentration, concentration after transportation, concentration after storage in a market, concentration at the time of purchase, concentration when at home, and concentration at the time of consumption) were analyzed. As a result of the simulation, in natural cheese, the initial concentration was −2.35 Log CFU/g, and concentration at the final stage (at the time of consumption) was −2.31 Log CFU/g (data not shown). This result indicates that non-EHEC E. coli in natural cheese may not grow during distribution and storage under the conditions in Korea. In addition, non-EHEC E. coli growth probability in processed cheese was similar to that in natural cheese (data not shown). Moreover, the results of comparison of the initial concentration with final concentration indicate that none of the 10,000 iterations could yield more than 0 Log CFU/g at the point of final concentration (Fig. 4).

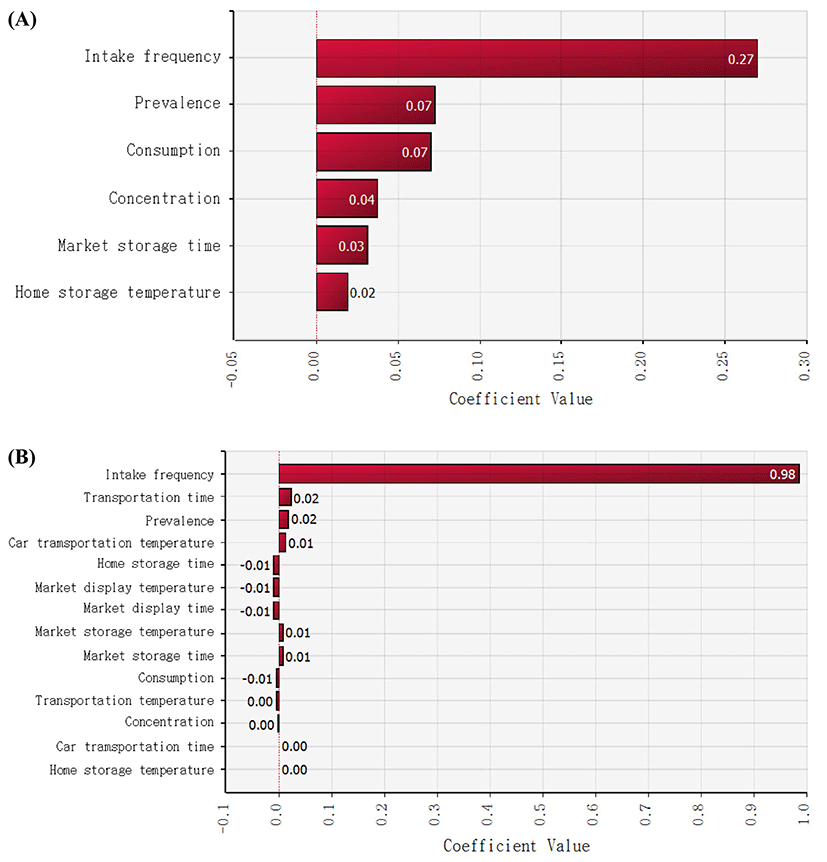
kosfa-37-4-579-f004
Fig. 4. The regression coefficient (A) and the correlation coefficient (B) values for the sensitivity risk factor affecting the probability of illness per person per day as a result of consumption of natural cheese.
Download Original Figure
The dose-response model and risk characterization

After cheese consumption, to estimate the probability of non-EHEC E. coli foodborne illness, the Beta-Poisson model (α = 2.21×10−1, N50 = 6.85×107) was used (Powell et al., 2000). Subsequently, the simulation model was prepared with the values of input variables such as non-EHEC E. coli prevalence, temperature, and time for distribution and display in markets, and home storage, the amount of cheese consumption, and intake frequency as presented Tables 1 and 2. The simulations were conducted by random sampling from the distribution described above for 10,000 iterations, and the mean probabilities of a non-EHEC E. coli outbreak as a result of cheese consumption per person per day in Korea were 1.36×10−7 and 2.12×10−10 for natural and processed cheese, respectively (Table 3), which are higher than the risk (7.84×1010) of S. aureus foodborne illness per person per day as a result of natural cheese consumption and the risk (3.64×10−9 to 1.30×10−7) of listeriosis per person per day as a result of eating lettuce at a restaurant in Korea (Ding et al., 2013; Lee et al., 2015). These results indicate that natural cheese poses a high risk of a non-EHEC E. coli outbreak as compared to processed-cheese-related and S. aureus-related foodborne illnesses as a result of natural cheese consumption and listeriosis as a result of lettuce consumption in Korea. In addition, sensitivity analysis revealed that intake frequency was the most influential factor for this risk, whereas the other factors such as storage temperature and time were not obviously related (Fig. 5).

Table 3. Probability of foodborne illness caused by Escherichia coli per person per day as a result of consumption of natural and processed cheeses
Probability of illness/(person·d) 5% 25% 50% 95% 99% Maximum Mean
Natural cheese 0 0 0 0 3.34×10−6 2.26×10−4 1.36×10−7
Processed cheese 0 0 0 0 4.59×10−9 1.20×10−7 2.12×10−10
Download Excel Table

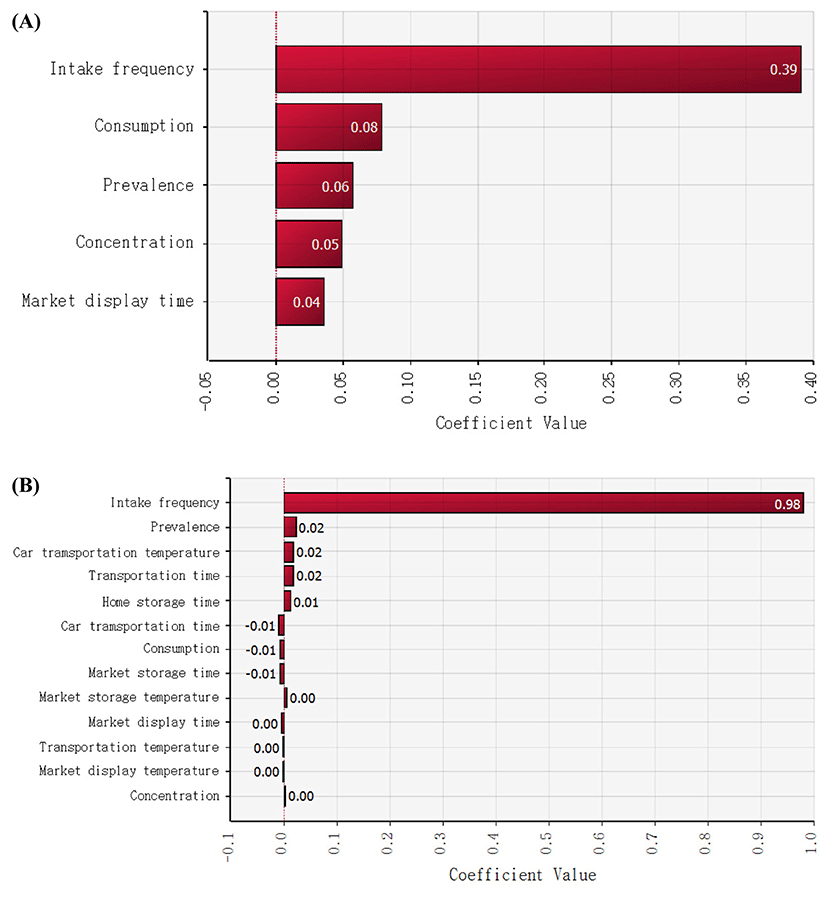
kosfa-37-4-579-f005
Fig. 5. The regression coefficient (A) and the correlation coefficient (B) values for the sensitivity risk factor affecting the probability of illness per person per day as a result of consumption of processed cheese.
Download Original Figure

Thus, our results indicate that non-EHEC E. coli cannot grow in natural and processed cheeses under the present distribution and storage conditions, and that a different factor is more important for the risk of illness. Consumption frequency of processed cheese is lower than that of natural cheese, if we assume that the consumption amount of natural and processed cheese is similar. Accordingly, processed cheese poses a lower risk than natural cheese for non-EHEC E. coli.

Conclusion

The risk of a non-EHEC E. coli outbreak via cheese consumption seems to be low for natural and processed cheese in Korea, and the intake frequency of cheese is the most influential factor for this risk. In addition, the microbial risk assessment model that we developed in this study can be useful for quantitative risk assessment.

Acknowledgements

This research was supported by a grant (13162MFDS927) from the Ministry of Food and Drug Safety in 2013.

References

1.

Baranceli G. V., Oliveira C. A., Corassin C. H., Camargo T. M., Santos M. G., Novotny L. C. M., Porto E. Occurrence of Escherichia coli and coliform in Minas cheese plants from Sãn Paulo, Brazil. J. Adv. Dairy Res. 2014; 2:1-4.

2.

Baranyi J., Roberts T. A. A dynamic approach to predicting bacterial growth in food. Int. J. Food Microbiol. 1994; 23:277-294.

3.

Gort’s cheese products of salmon arm suspected in E. coli outbreak. 2013Available from: http://www.bccdc.ca/resourcematerials/newsandalerts/healthalerts/2013HealthAlerts/E.+Coli+Investigation+-+Foodborne+Illness.htmAccessed Jun. 09, 2017

4.

Bonyadian M., Moshtaghi H., Taheri M. A. Molecular characterization and antibiotic resistance of enterotoxigenic and enteroaggregative Escherichia coli isolated from raw milk and unpasteurized cheeses. In: Vet. Res. Forum. 2014; 5 p. 29-34.

5.

CDC (Centers for Disease Control and Prevention) Multistate outbreak of E. coli O157:H7 infections associated with cheese (final update). 2010Available from: http://www.cdc.gov/ecoli/2010/bravo-farms-cheese-11-24-10.htmlAccessed Jun. 09, 2017

6.

Codex Principles and guidelines for the conduct of microbiological risk assessment. CAC/GL-30. 1999Available from: http://www.fao.org/docs/eims/upload/215254/CAC_GL30.pdfAccessed Dec. 28, 2015

7.

Ding T., Iwahori J., Kasuga F., Wang J., Forghani F., Park M. S., Oh D. H. Risk assessment for Listeria monocytogenes on lettuce from farm to table in Korea. Food Control. 2013; 30:190-199.

8.

EC (Commission of the European Communities) Commission regulation of on microbiological criteria for foodstuffs. SANCO/4198/2001 Rev. 19. 2005Available from: http://ec.europa.eu/food/food/biosafety/salmonella/reg_microbiological_criteria-foodstuffs_en.pdfAccessed Jun. 09, 2017

9.

EPA (Environmental Protection Agency) Microbial risk assessment guideline: Pathogenic microorganisms with focus on food and water. 2012EPA/100/J-12/001

10.

FDA (U. S. Food and Drug Administration) Guidance for FDA staff, compliance policy guide, CPG 7106.08. 2009Available from: http://www.fda.gov/downloads/ICECI/ComplianceManuals/CompliancePolicyGuidanceManual/UCM192468.pdfAccessed May 10, 2017

11.

FSANZ (Food Standard and New Zealand) Microbiological risk assessment of raw milk cheese. 2009Available from: https://www.foodstandards.gov.au/code/proposals/documents/P1007%20PPPS%20for%20raw%20milk%201AR%20SD3%20Cheese%20Risk%20Assessment.pdfAccessed Oct. 11, 2016

12.

Griffin P. M., Tauxe A. V. The epidemiology of infections caused by Escherichia coli O157:H7, other enterohemorrhagic E. coli and the associated haemolytic uremic syndrome. Epidemiol. Rev. 1991; 13:60-98.

13.

Haran K. P., Gooden S. M., Boxrud D., Jawahir S., Bender J. B., Sreevatsan S. Prevalence and characterization of Staphylococcus aureus, including methicillin-resistant Staphylococcus aureus, isolated from bulk tank milk from Minnesota dairy farms. J. Clin. Microbiol. 2011; 50:688-695.

14.

Health Canada Health products and food branch (HPFB) standards and guidelines for microbiological safety of food. 2008Available from: http://www.gftc.ca/knowledge-library/file.aspx?id=73bf2c7d-7beb-45d2-a0d1-81456a71db62Accessed May 10, 2017

15.

Hong S. H., Park N. Y., Jo H. J., Ro E. Y., Ko Y. M., Na Y. J., Park K. C., Choi B. G., Min K. J., Lee J. K., Moon J. S., Yoon K. S. Risk ranking determination of combination of foodborne pathogens and livestock or livestock products. J. Food Hyg. Safety. 2015; 30:1-12.

16.

Honish L., Predy G., Hislop N., Chu L., Kowalewska-Grochowska K., Trottier L., Kreplin C., Zazulak I. An outbreak of E. coli O157:H7 hemorrhagic colitis associated with unpasteurized gouda cheese. Can. J. Public Health. 2005; 96:182-184.

17.

Jo C., Kim H. J., Kim D. H., Lee W. K., Ham J. S., Byun M. W. Radiation sensitivity of selected pathogens in ice cream. Food Control. 2007; 18:859-865.

18.

Johnson N. L., Kotz S., Balakrishnan N. Continuous Univariate Distributions. 2nd ed.Wiley. 1995; 2 Chapter 21: Beta Distributions..

19.

KDC (Korea Dairy Committee) Domestic statistics. 2016Available from: http://www.dairy.or.kr/jsp/layout/LayoutControlCtrl.jsp?ACT_CD=MAIN&INDEX_UPPERMENU_CODE=domestic&INDEX_MENU_CODE=domestic_cs_condition&INDEX_MENU_DEPTH=2Accessed Sep 05, 2016

20.

Lee H., Kim K., Choi K. H., Yoon Y. Quantitative microbial risk assessment for Staphylococcus aureus in natural and processed cheese in Korea. J. Dairy Sci. 2015; 98:5931-5945.

21.

MFDS (Ministry of Food and Drug Safety) Escherichia coli risk profile. 2010; p. 4-11.

22.

MFDS (Ministry of Food and Drug Safety) Quantitative standard establishment and risk assessment of foodborne pathogens on cheese. MFDS research report. 2013

23.

Najand L. M., Ghanbarpour R. A study on enteropathogenic Escherichia coli isolated from domestic Iranian soft cheese. Vet. Arch. 2006; 76:531-536.

24.

Nataro J. P., Kaper J. B. Diarrheagenic Escherichia coli. Clin. Microbiol. Rev. 1998; 11:142-201.

25.

Olsvik Ø., Wasteson Y., Lund A., Hornes E. Pathogenic Escherichia coli found in food. Int. J. Food Microbiol. 1991; 12:103-113.

26.

Perrin F., Tenenhaus-Aziza F., Michel V., Miszcyzycha S., Bel N., Sanaa M. Quantitative risk assessment of haemolytic and uremic syndrome linked to O157:H7 and non-O157:H7 Shiga-toxin producing Escherichia coli strains in raw milk soft cheeses. Risk Anal. 2015; 35:109-128.

27.

Powell M. R., Ebel E., Schlosser W., Walderhaug M., Kause J. Dose-response envelope for Escherichia coli O157:H7. Quantitative Microbiol. 2000; 2:141-163.

28.

Ratkowsky D. A., Olley J., McMeekin T. A., Ball A. Relationship between temperature and growth rate of bacterial cultures. J. Bacteriol. 1982; 149:1-5.

29.

Reitsma C. J., Henning D. R. Survival of enterohemorrhagic Escherichia coli O157:H7 during the manufacturing and curing of Cheddar cheese. J. Food Prot. 1996; 59:460-464.

30.

Tekinsen K. K., Özdemir Z. Prevalence of foodborne pathogens in Turkish Van otlu (Herb) cheese. Food Control. 2006; 17:707-711.

31.

Thayer D. W., Boyd G., Kim A., Fox J. B, Farrell H. M. Fate of gamma-irradiated Listeria monocytogenes during refrigerated storage on raw or cooked turkey breast meat. J. Food Prot. 1998; 61:979-987.

32.

Vose D. J. The application of quantitative risk assessment to microbial food safety. J. Food Prot. 1998; 61:640-648.

33.

Yoon J. W. Non-O157 shiga-toxigenic Escherichia coli: Under-rated pathogen. Safe Food. 2009; 4:33-36.

34.

Zinke C., Winter M., Mohr E., Kromker V. Occurrence of methicillin-resistant Staphylococcus aureus in cheese produced in German farm-dairies. Adv. Microbiol. 2012; 2:629-633.

Food Science of Animal Resources
#806, Hangang Hyundai HYEL, 213-12, Saechang-ro, Yongsan-gu, Seoul 04376, Korea
Tel : +82-2-458-4594 | kosfa78@hanmail.net

Copyright © Korean Society for Food Science of Animal Resources. 2024. Powered by Guhmok