Introduction
Jerky is a nutritional snack with a high protein content and light weight, and thus it is consumed by many people (Holley, 1985). It is also easy to store because of its long shelf-life and low Aw (Calicioglu et al., 2003). However, outbreaks of foodborne illness have occurred in many countries (Eidson et al., 2000; Keene et al., 1997). These outbreaks may be caused by cross contamination during jerky processing, molding, packaging, and cutting. Also, most of jerkies are made in small companies, and these companies have difficulties for food hygiene management. Thus, foodborne pathogen growth need to be simulated in jerky for exposure assessment.
Staphylococcus aureus can produce enterotoxin, leading to foodborne intoxication (Le Loir et al., 2003). Generally, the symptoms of foodborne illness include abdominal cramps, vomiting, and diarrhea (Jones et al., 2002). S. aureus can grow under various conditions, such as a wide range of temperatures, pH, and low AW (Bergdoll, 1989; Schmitt et al., 1990) and most S. aureus isolates from food exhibit antimicrobial resistance (Can et al., 2017). The pathogen is commonly found on human skin (Otto, 2008), and may be cross-contaminated from human hands to jerky. Thus, there is high possibility for jerky contamination by S. aureus.
Predictive models are useful for estimating microbial growth or death in food using mathematical models (Zwietering et al., 1996). The purpose of a predictive model is to secure food safety in advance by identifying risk factors (Yoon, 2010). A primary model describes changes in bacterial cell counts over storage time to calculate kinetic parameters such as growth rate and lag phase duration (Ha et al., 2016). A secondary model describes the effects of environmental factors such as pH, AW, and temperature on kinetic parameters (Buchanan, 1993; Ha et al., 2016).
Therefore, the objective of this study was to develop mathematical models for describing the kinetic behavior of S. aureus in beef jerky.
Materials and Methods
S. aureus ATCC13565 was cultured in 10 mL of tryptic soy broth (TSB; BD Biosciences, Franklin Lakes, NJ, USA) at 37°C for 24 h. For subculture, 0.1 mL of the culture was transferred into 10 mL fresh TSB at 37°C for 24 h. The sample was centrifuged at 1,912×g and 4°C for 15 min and washed twice with phosphate-buffered saline (PBS: pH 7.4; 0.2 g of KH2PO4, 1.5 g of Na2HPO4·7H2O, 8.0 g of NaCl, and 0.2 g of KCl in 1 L of distilled water). The supernatants were discarded, and the cell pellets were resuspended in PBS. Cell suspensions were diluted with PBS to 3–4 Log CFU/mL for inoculation.
Seasoned beef jerky was purchased from an online shop in Korea. Ten-gram portions of the samples were placed into sterile filter bags (3M, St. Paul, MN, USA), and 0.1-mL aliquots of S. aureus were dotted on several places of the beef jerky surface for inoculation to obtain 3 Log CFU/g in the sample bags. The samples were rubbed 20 times and the sample bags were sealed, followed by aerobic storage at 10°C (600 h), 20°C (600 h), 25°C (480 h), 30°C (192 h), and 35°C (96 h). These time intervals were determined according to the time that S. aureus cell counts were below detection limit. Beef jerky samples were analyzed at different time intervals. Thirty milliliters of 0.1% buffered peptone water (BPW; BD Biosciences) were added to each sample and homogenized with a BagMixer (Interscience, St. Nom, France) for 90 s. The homogenates were serially diluted with BPW. The 0.1 mL of the diluents were plated onto Baird-Parker agar (MB Cell, Los Angeles, CA, USA) for S. aureus, and the plates were incubated at 37°C for 48 h. Typical colonies on the plates were counted, and the Weibull model was fitted to the S. aureus cell count data (Van Boekel, 2002).
where N0 is the initial cell count, ρ is the shape of the curve, and δ is the time required for the first decimal reduction. The polynomial model (δ=N0+a×T+b×T2) was used to evaluate the effect of storage temperature on δ.
S. aureus cell count data were obtained at 15°C and 23°C in additional experiments to evaluate the model performance. These observed data were compared to predicted data, which were calculated from the predictive model. The differences between the observed and predicted data were quantified by calculating the root mean square error (RMSE) (Baranyi et al., 1996);
where n represents the number of data points.
Results and Discussion
Because various types of jerky are available made from different meat types and marinades, the behavior of S. aureus may differ among jerkies. Thus, a predictive model should be developed for each jerky type to describe the behavior of S. aureus. However, this effort requires a long time and is costly. Developing a model with the jerky type, allowing the highest S. aureus growth, may be appropriate for the most severe case, which would save time and expense. To determine a model for developing a predictive model, we examined the pH and water activities of 75 samples of 15 original jerky products (Table 1) and 50 samples of 10 seasoned jerky products (Table 2). The pH values were highly similar among the samples (6.13–6.17), but the water activities were higher in the seasoned jerky (0.810±0.045) than in the original jerky (0.656±0.134) (Tables 1 and 2). The 10-seasoned jerky products contained sodium nitrite, potassium sorbate, and sodium sorbate. The growth of most bacteria is inhibited when AW is reduced. Particularly, the growth of S. aureus is inhibited when AW is less than 0.850 in an aerobic environment (Jay 1992). Holley (1985) indicated that the AW of jerky was 0.620 when stored at refrigeration temperature for 26 days, but there was no significant difference in S. aureus cell counts compared to the cell counts on day 0. This result suggests that S. aureus can survive in beef jerky even if AW is less than 0.850. Additionally, Lee et al. (2016) indicated that S. aureus did not grow under vacuum conditions. Hence, we developed predictive models using the seasoned beef jerky products as a model product under aerobic conditions to predict the most severe case of S. aureus growth.
S. aureus-inoculated seasoned beef jerky samples were stored in aerobic packaging at 10°C, 20°C, 25°C, 30°C, and 35°C. The cell counts were gradually decreased at 10°C and 20°C, but a tail effect was observed at 10°C and S. aureus cell counts survived through the end of storage at 20°C (Fig. 1). However, the S. aureus cell counts greatly decreased as the temperature was increased to 25°C, 30°C, and 35°C (Fig. 1). The cell counts decreased to below the detection limit (0.48 Log CFU/g) after 432, 144, and 120 h at 20°C, 25°C, and 30°C, respectively (Fig. 1).
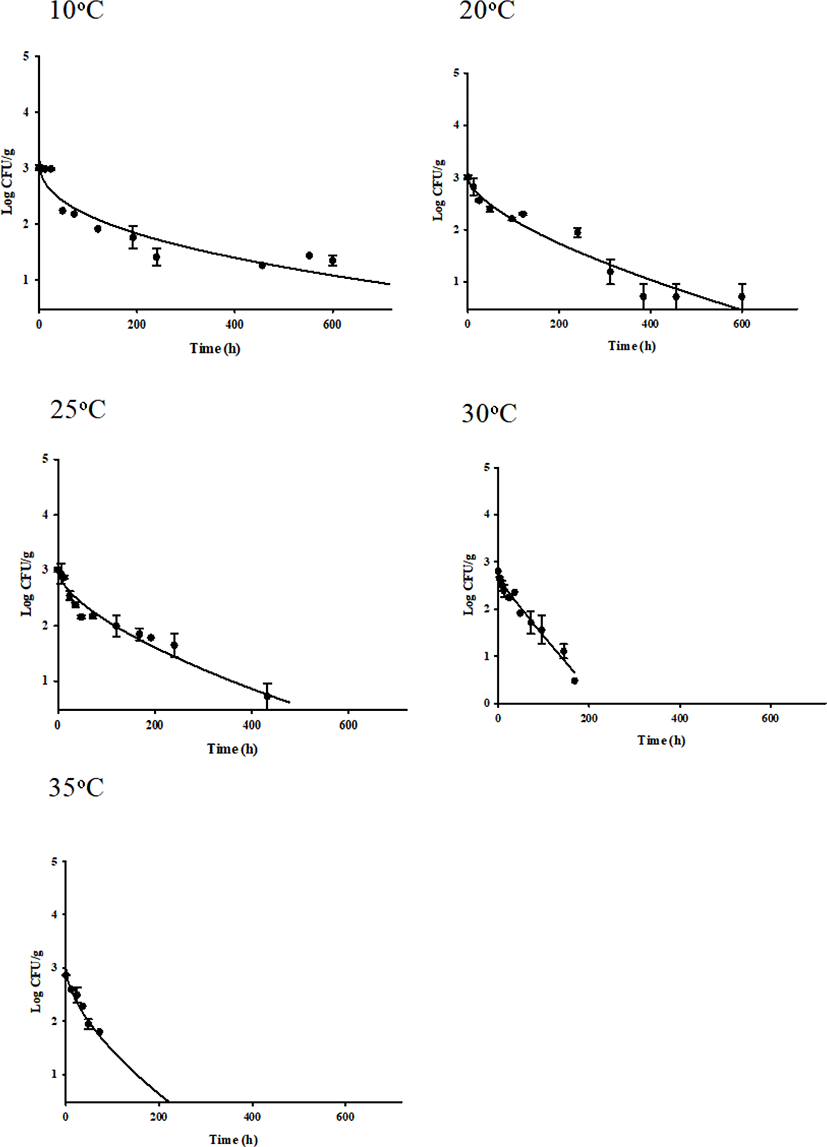
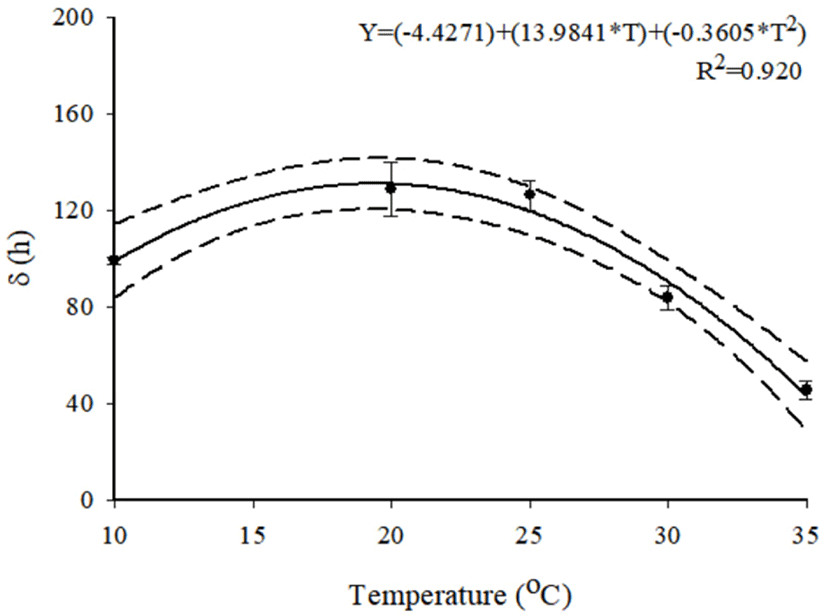
To describe the kinetic behavior of S. aureus in beef jerky, primary models were developed and R2 values ranged from 0.868 to 0.967, indicating that the developed primary models were appropriate. These primary models showed that the δ values generally decreased as temperature increased (Table 3). This result agrees with those of Moon et al. (2017) who showed that S. aureus in dried julienned squid survived longer at 10°C than at 35°C. These results suggest that if S. aureus is contaminated in beef jerky stored at low temperature, the pathogen can survive for a long time and cause food safety issues. Because S. aureus cell counts decreased as shown in Fig. 1, the ρ values were less than 1, indicating that all curves were concave (Coroller et al., 2006). To evaluate the effect of ρ on temperature, a secondary model was developed and R2 was 0.920 (Fig. 2), indicating that the developed model was appropriate. The equation was δ=(−4.4271)+(13.9841×T)+(−0.3605×T2) (Fig. 2). The secondary model showed that the δ values were generally influenced by temperature. The RMSE value was calculated to evaluate model performance. A value close to zero indicates that the predicted values are the same as the observed values (Kim et al., 2017). In this study, the value was 0.326, indicating that the developed models were appropriate for describing the kinetic behavior of S. aureus in beef jerky.
In conclusion, the developed predictive models are useful in describing the kinetic behavior of S. aureus in beef jerky. Additionally, because the model beef jerky was selected according to the most optimum growth conditions for S. aureus, the developed models can be applied to other jerkies. Although beef jerky has a low AW, if S. aureus is contaminated in the beef jerky, the cells can survive for a long period at low temperature and cause food safety issues. Therefore, beef jerky should not be considered as a microbiologically safe food and thus, cross-contamination should be controlled during processing.













